Livello: Avanzato
In questo capitolo trarrò informazioni da:
- La pagina inglese di Wikipedia circa i sistemi-L: http://en.wikipedia.org/wiki/L-System.
- Il libro “The Algorithmic Beauty of Plants” scritto da by Przemyslaw Prusinkiewicz e Aristid
Lindenmayer.
Questa sezione tratterà dei sistemi Lindemayer o sistemi L introdotti e sviluppati nel 1968 dal biologo teoretico
Lindenmayer. Un sistema-L è un sistema di regole e simboli utilizzato per modellizare i processi di crescita dello
sviluppo delle piante ma anche è anche capace di modellizare la morfologia di una varietà di organismi. Il concetto
principale dei sistemi L è il “regole di sostituzione”. Questa tecnica è utilizzata per sostituire alcune condizioni
iniziali utilizzando alcune regole.
Un sistema-L è una grammatica formale con:
- un alfabeto V : l’insieme delle variabili del sistema-L. V * rappresenta l’insieme delle “parole” che
possiamo generare con qualsiasi simbolo preso dall’alfabeto V , e V + l’insieme delle “parole” con almeno
un simbolo.
- Un insieme di valori costanti S. Alcuni di questi simboli sono in comune a tutti i sistemi L (in
particolare con le tartarughe).
- Un assioma di partenza ω preso da V +, è lo stato iniziale.
- Un insieme di regole di produzione P dei simboli V .
Questo sistema-L è definito come una ennupla (o tupla) {V,S,ω,P}.
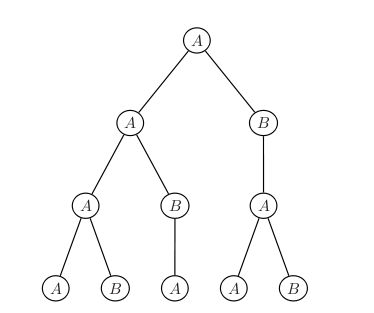
Consideriamo il seguente sistema-L:
- Alfabeto : V = {A,B}
- Constanti : S = {∅}
- Assioma iniziale: ω = A
- Regole :
Le due regole di produzione sono regole di sostituzione. Ad ogni passo il simbolo A è sostituito dalla
sequenza AB ed il simbolo B è sostituito da A. Ecco le prime iterazioni di questo sistema-Lindemayer:
- A
- AB
- ABA
- ABAAB
Ok, ok ma concretamente? Leggiamo la prossima sezione!
Questo primo esempio aiuta a capire cos’è un sistema-L ma ancora non ci fa capire il rapporto con la nostra
tartaruga e LOGO…
Qui diventa interessante: tutte le parole che abbiamo costruito non hanno significato. Definiremo per ciascuna
lettera della sequenza una azione da eseguire da parte della tartaruga e disegneremo con questo metodo disegni 2D e
3D.
- F : Av di un passo di una unità (∈ V )
- + : Gira l’angolo a sinistra α (∈ S).
- - : Gira l’angolo a destra α (∈ S).
- & : Beccheggia giù α (∈ S).
- ^: Beccheggia sù α (∈ S).
- \: Rollio a sinistra α (∈ S).
- ∕: Rollio a destra α (∈ S).
- |: Torna indietro. In XLOGO: DX 180
Per esempio se α = 90 con un passo di 10 unità abbiamo:
|
|
|
|
|
|
|
|
|
| Simbolo | F | + | - | & | ^ | \ | ∕ | | |
|
|
|
|
|
|
|
|
|
| Comando XLOGO | Av 10 | SX 90 | DX 90 | BG 90 | BS 90 | RSX 90 | RDX 90 | DX 180 |
|
|
|
|
|
|
|
|
|
| |
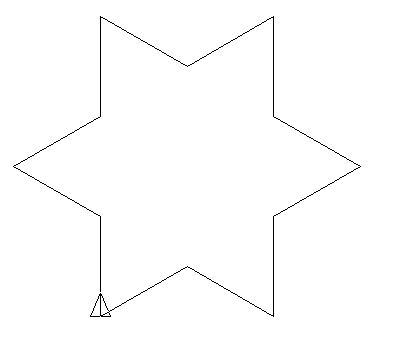
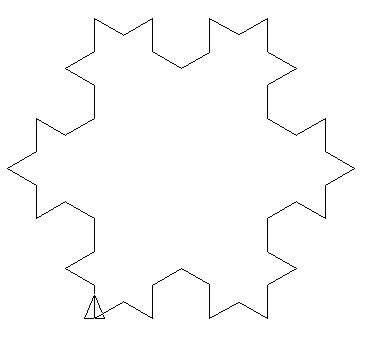
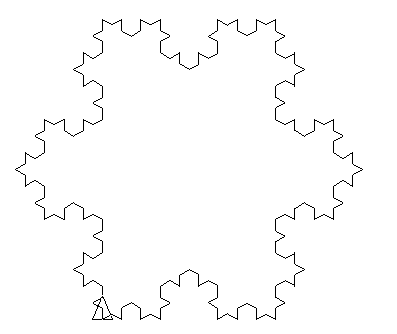
Consideriamo il sistema-L:
- Stato iniziale: F --F --F --
- Regole di produzione: F → F + F --F + F
- Angolo α = 60∘, l’unità del passo è divisa per 3 tra ciascuna iterazioni.
Prime iterazioni:
Programma XLOGO:
Codice 15.1: Il fiocco di neve
Per FioccoDiNeve :p AssegnaVar "unit 300/Potenza 3 :p-1 Ripeti 3 [f :p-1 DX 120] Fine Per f :p Se :p=0 [Av :unit Ferma] f :p-1 SX 60 f :p-1 DX 120 f :p-1 SX 60 f :p-1 Fine
Dato questo nuovo sistema-L:
- Stato iniziale: F - F - F - F
- Regole di produzione: F → F - F + F + FF - F - F + F
Queste sono le prime rappresentazioni utilizzando α = 90 e dimensionando la dimensione del passo (:unita) in
modo che la figura risultante abbia dimensioni costanti.
E’ molto semplice creare un programma Logo per generare questi disegni:
Codice 15.2: Curva quadratica di Van Koch
# p rappresenta l’ordine per koch :p # la figura finale avra’ una dimensione massima di 600x600 AssegnaVar "unita 300/Potenza 4 :p-1 Ripeti 3 [f :p-1 SX 90] f :p-1 fine # regole di sostituzione per f :p Se :p=0 [Av :unita Ferma] f :p-1 SX 90 f :p-1 DX 90 f :p-1 DX 90 f :p-1 f :p-1 SX 90 f :p-1 SX 90 f :p-1 DX 90 f :p-1 fine
- Stato iniziale: F
- Regole di produzione:
Codice 15.3: Curva del dragone
per a :p Se :p=0 [Av :unit Ferma] a :p-1 SX 90 b :p-1 SX 90 fine per b :p Se :p=0 [Av :unit Ferma] DX 90 a :p-1 DX 90 b :p-1 fine per dragon :p AssegnaVar "unit 300/8/ :p a :p fine
Il seguente esempio genererà una curva 3D di Hilbert. E’ una curva singolare perché riempie perfettamente un cubo
quando aumentiamo le iterazioni.
Questo è il sistema-L da considerare:
- Stato iniziale: A
- Angolo α = 90∘, l’unità del passo è divisa per 2 tra due iterazioni.
- Regole di produzione:
|
A → B - F + CFC + F - D&F^D - F + &&CFC + F + B∕∕ |
B → A&F^CFB^F^D^^ - F - D^|F^B|FC^F^A∕∕ |
C →|D^|F^B - F + C^F^A&&FA&F^C + F + B^F^D∕∕ |
D →|CFB - F + B|FA&F^A&&FB - F + B|FC∕∕ |
|
|
Codice 15.4: Curva 3D di Hilbert
per hilbert :p PS 3D AssegnaVar "unit 400/Potenza 2 :p FineLinea ImpSP :unit/2 a :p InizioLinea VistaPoligono3D fine per a :p Se :p=0 [Ferma] b :p-1 DX 90 Av :unit SX 90 c :p-1 Av :unit c :p-1 SX 90 Av :unit DX 90 d :p-1 BG 90 Av :unit BS 90 d :p-1 DX 90 Av :unit SX 90 BG 180 c :p-1 Av :unit c :p-1 SX 90 Av :unit SX 90 b :p-1 RDX 180 fine per b :p Se :p=0 [Ferma] a :p-1 BG 90 Av :unit BS 90 c :p-1 Av :unit b :p-1 BS 90 Av :unit BS 90 d :p-1 BS 180 DX 90 Av :unit DX 90 d :p-1 BS 90 DX 180 Av :unit BS 90 b :p-1 DX 180 Av :unit c :p-1 BS 90 Av :unit BS 90 a :p-1 RDX 180 fine per c :p Se :p=0 [Ferma] DX 180 d :p-1 BS 90 DX 180 Av :unit BS 90 b :p-1 DX 90 Av :unit SX 90 c :p-1 BS 90 Av :unit BS 90 a :p-1 BG 180 Av :unit a :p-1 BG 90 Av :unit BS 90 c :p-1 SX 90 Av :unit SX 90 b :p-1 BS 90 Av :unit BS 90 d :p-1 RDX 180 fine per d :p Se :p=0 [Ferma] DX 180 c :p-1 Av :unit b :p-1 DX 90 Av :unit SX 90 b :p-1 DX 180 Av :unit a :p-1 BG 90 Av :unit BS 90 a :p-1 BG 180 Av :unit b :p-1 DX 90 Av :unit SX 90 b :p-1 DX 180 Av :unit c :p-1 RDX 180 fine
E le prime iterazioni:
Bello, non è vero?