Ĉi tie, ni lernos desegni kvadraton, egallateran trilateron, regulan kvinlateron, ktp.
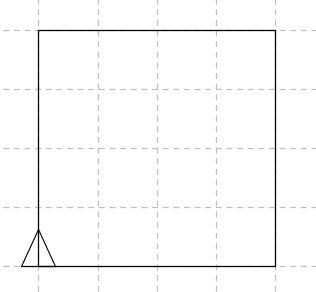
Unu reta ĉelo reprezentas 50 testudajn paŝojn. Por desegni la apudan kvadraton, oni do tajpu:
an 200 dn 90 an 200 dn 90 an 200 dn 90 an 200 dn 90
|
Oni rimarku ke oni ripetas 4 fojojn la saman instrukcion, do jen sintakso pli rapida:
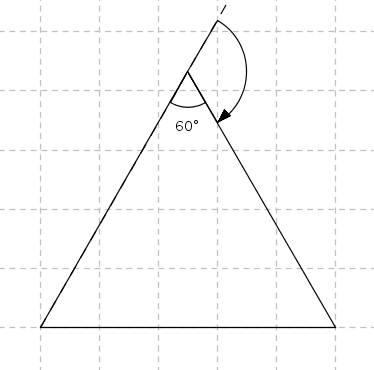
Ĉi tie, ĉelo reprezentas 30 testudpaŝojn. Ni vidos kiel desegni tiun egallateran trilateron kun lateroj de 150
testudpaŝoj. La instrukcio similos ion tian:
Restas kalkuli la bonan angulon. En egallatera trilatero, l’ anguloj havas ĉiuj 60 gradojn. Ĉar la
testudo turniĝas ekster la trilatero, l’ angulo validas 180 − 60 = 120 gradojn. L’ instrukcio estas do:
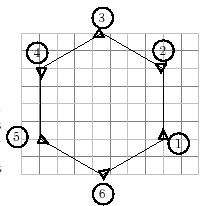
Ĉi tie, ĉelo reprezentas 20 testudpaŝojn.
Oni rimarku ke dum ĝia moviĝo, la testudo efektivigas kompletan turniĝon (ĝi ekiras adresita al supro, fine
ĝi revenas en tiun saman pozicion). Tiu turniĝo je 360 gradoj efektiviĝos post 6 etaĝoj. Tial, je ĉiu fojo, ĝi
turniĝas je 360∕6 = 60∘.
L’ instrukcio estu do: ripetu 6 [an 80 dn 60]
Efektive, ripetante la malgrandan pensadon antaŭan, oni
rimarku ke, por desegni plurlateron je n lateroj, l’ angulon oni kalkulu per divido de 360 per n. Por
ekzemplo:
- Por grafiki regulan kvinlateron je latero 100:
ripetu 5 [an 100 dn 72] (360:5=72)
|
- Por grafiki regulan naŭlateron je latero 20:
ripetu 9 [an 20 dn 40] (360:9=40)
|
- Por grafiki regulan ee... 360-lateron je latero 2 (ĝi ja similas cirklon!):
- Por grafiki seplateron je latero 120:
ripetu 7 [an 120 dn 360/7]
|